Abstract:
The Deep Learning model is derived, or say inspired from neural network(NN). I derived the theory and then implement it with python to build the first extensionable NN model.
Content:
Firstly, I’ll give the convention used in the devivation, and then deduce the math with the convention, later the code implemention is given and in the last, the application.
Structure
for this network system, we assume the structure is like: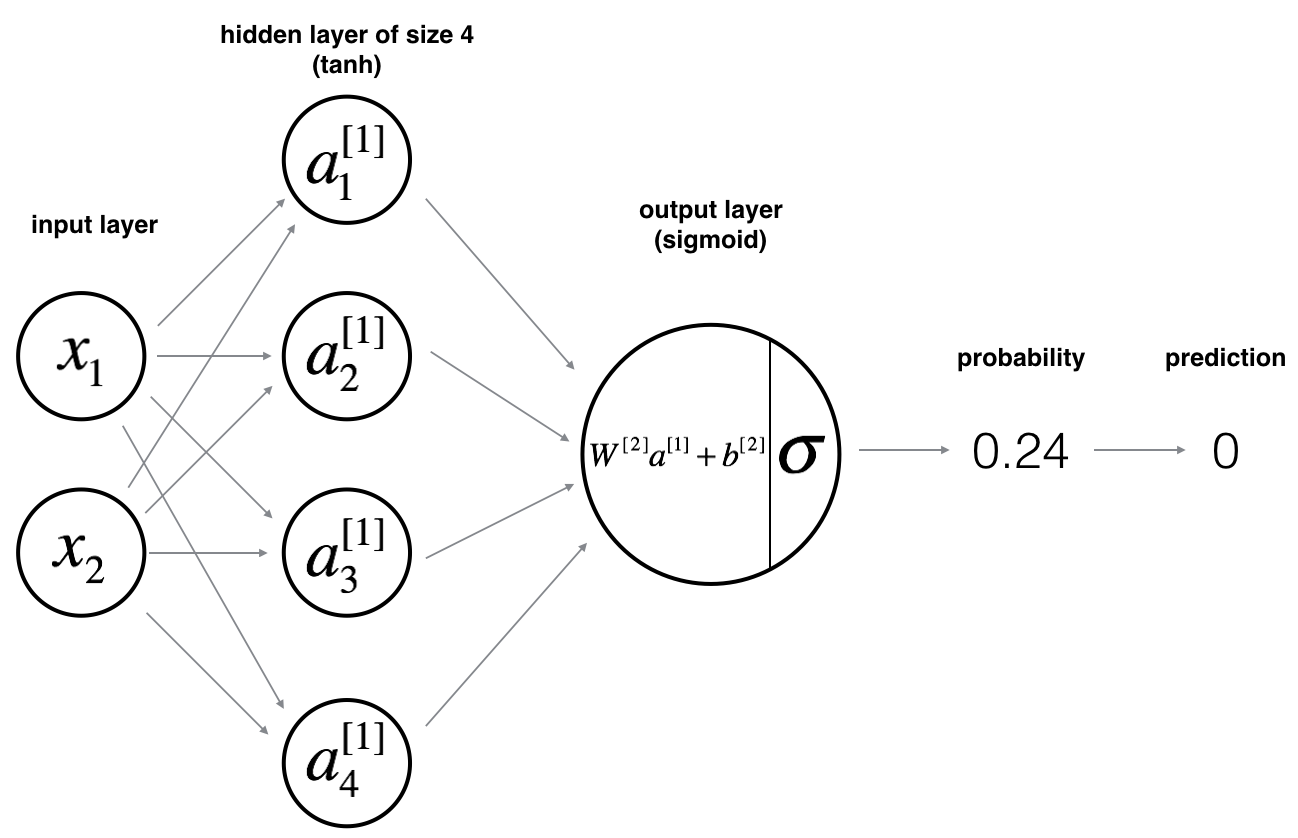
where $n^{[i]}$ is the $i$ layer hidden unit number; $x$ is input data with $n^{[0]}$ features and m examples in total; $\hat{y}$ is estimated output, usually $n^{[2]} = 1$ for binary classification system.
Conventions
- Assuming we apply sigmoid function $\sigma(z)=\frac{1}{1+e^{-Z}}$ for activate function for all layers.
- $y$ is the real ouput/label for data with $y.shape=(n^{[2]},m)$.
- Broadcasting convention in python is applied automaticlly when needed(such as braodcasting $1$ for $1-y$ or braodcasting $b^{[1]}$ for $W^{[1]}A^{[0]}+b^{[1]}$).
- We apply:
- $\cdot$ for matrix dot production,
- $\times$ for real value production
- $*$ for eliment wised matrix production.
Forward Propogation
Giving input $A^{[0]} = x$, and randomly initialized parameters $W^{[1]}$, $b^{[1]}$, $W^{[2]}$, $b^{[2]}$. We can calculate $Z^{[1]}$, $A^{[1]}$, $Z^{[2]}$, $A^{[2]}$.
And final cost function:
Backward Propogation
In order to do gradient decent optimization, we need to calculate $\frac{\partial \mathcal{J}}{\partial W^{[2]}}$, $\frac{\partial \mathcal{J}}{\partial b^{[2]}}$, $\frac{\partial \mathcal{J}}{\partial W^{[1]}}$,$\frac{\partial \mathcal{J}}{\partial b^{[1]}}$. Then we can apply them to update $W^{[1]}$, $W^{[2]}$, $b^{[1]}$, $b^{[2]}$.
chain rule
We apply chain rule for gradient calculation as following:
derivative for sigmoid function and loss function
Firstly, we get the derivative for scalar activate function and loss function. Only considering one example so that $z$ and $a$ are both real value other than vector:
matrix derivative
Now, we’re ready to calculate matrix derivative. For matrix calculation, We’ll apply Einstein sumption convention.
We introduce a symbol $\epsilon_{ij}= 1$ when $j=i$, $\epsilon_{ij} = 0$ when $j\neq i$. we denote the row $i$, column $j$ eliment in matrix $M$ as $M_{ij}$.
Since we apply broadcasting, we have $b^{[l]}_{ij} = b^{[l]}_{ik}$ for any $i, j, k, l$. So we could denote $b^{[l]}_i = b^{[l]}_{ij}$. And all the derivative $db^{[l]}_{ij}$ could contribute(add up) to $db^{[l]}_{i}$. In other words, $db^{[l]}_{i} = \sum_{j=1}^{m}db^{[l]}_{ij}$
Based on Einstein sumption convention, above equation can be transfered as matrix equation:
python code
For python code variable name convenient, we denote:
Then the python code for getting them is:
db2 = 1.0/m * np.sum(A2 - Y, axis=1, keepdims=True)
dw2 = 1.0/m * np.dot(A2 - Y, A1.T)
db1 = 1.0/m * np.sum(np.dot(W2.T, A2 - Y) * (A1 * (1 - A1)), axis=1, keepdims=True)
dw1 = 1.0/m * np.dot(np.dot(W2.T, A2 - Y) * (A1 * (1 - A1)), X.T)
cache for computational benefit
From above, there are many repetitive calculation. such as $A^{[2]} - Y$, which appear everywhere. We could cache such frequently used values to save calculation. Actually, from the equation above it’s easy to see that $\frac{\partial \mathcal{J}}{\partial Z^{[1]}}$ and $\frac{\partial \mathcal{J}}{\partial Z^{[2]}}$ are the variables worth to cache. Because:
It’s easy to know, that:
So:
So the pytho code with cache is:
dZ2 = (1.0/m) * (A2 - Y)
db2 = np.sum(dZ2, axis=1, keepdims=True)
dw2 = np.dot(dZ2, A1.T)
dZ1 = np.dot(W2.T, dZ2) * (A1 * (1 - A1)
db1 = np.sum(dZ1, axis=1, keepdims=True)
dw1 = np.dot(dZ1, X.T)
Extend layer number and hidden unit number
unit number
In our above deduction, we actually not limit(hard code) the layer unit number, we only apply $n^{[l]}$ to represent the unit number for layer $l$. Even for the input layer $X$ and output layer $Y$. So you can choose any unit number you like, our equation will still apply to them.
Just to address that, if you choose more that one unit for output layer $Y$, then it could be multi-classification system other than binary classification. But then you may need to redefine the cost function and lost function(original may not work well). If you want to extend output layer unit and redefine loss function $\mathcal{L}$, just remember to replace $\frac{\partial \mathcal{J}}{\partial Z^{[n]}}$ carefully in the equation, then all will work fine.
layer number
In our above deduction, we limit the layer number to be 2(exclude input layer). But we could do the same calculation for 3, 4 or n layer system. It’s not hard to get the formula for n layer network by mathematical induction. In following, we denote $A^{[0]}=X$, $A^{[n]}=\hat Y$, $Y$ to be the real label from data. And assuming only one unit in output layer $Y$, so apply original $\mathcal{L}$ and $\mathcal{J}$.
formula
forward propogation:
And final cost function:
backward propogation:
python code
We assume provided W=[0, W1, W2, …, Wn], b=[0, b1, b2, …, bn].
import package:1
2
3
4
5import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
np.random.seed(1) # set a seed so that the results are consistent
forward propogation:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17# sigmoid function
def sigmoid(x):
return 1/(1+np.exp(-x))
# forward to get A
def forward(X, b, W, layer_number):
A0 = X
n = layer_number
A = [A0]
for i in range(1, n+1):
A.append(sigmoid(np.dot(W[i], A[i-1]) + b[i])) #
return A # A = [A0, A1, A2 ... An]
# calculate cost based on A
def cal_cost(An, Y):
m = Y.shape[1] # number of examples
cost = -(1.0)/m * np.sum(np.multiply(np.log(An), Y) + np.multiply((1 - Y), np.log(1 - An)))
cost = np.squeeze(cost) # makes sure cost is the dimension we expect. like [[17]] into 17
return cost
backward propogation:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23# backward to get db, dW
def backward(W, A, Y, layer_number):
dZ = None #for keeping the latest dZi
db = [0]
dW = [0]
n = layer_number
m = Y.shape[1]
for i in range(n, 0, -1):
if i == n:
dZ = 1.0/m * (A[i] - Y) # since A=[A0, A1, ..An], so An = A[n]
else:
dZ = np.dot(W[i+1].T, dZ) * (A[i] * (1 - A[i])) # giving W=[0, W1, W2, ... Wn], so Wn = W[n]
db.insert(1, np.sum(dZ, axis=1, keepdims=True)) # db=[0, dbi, dbi+1, ..., dbn]
dW.insert(1, np.dot(dZ, A[i-1].T)) # dW=[0, dWi, dWi+1, ..., dWn]
return db, dW # now db=[0, db1, db2, ..., dbn], dW=[0, dW1, dW2, ..., dWn]
# update d and W
def update_params(db, dW, b, W, learning_rate, layer_number):
n = layer_number
for i in range(1, n+1):
b[i] = b[i] - learning_rate * db[i]
W[i] = W[i] - learning_rate * dW[i]
return b, W
bulid model:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51# initialize d and W
def inital_params(X, Y, hidden_layer_units):
np.random.seed(2)
b = [0]
W = [0]
n_last = X.shape[0]
# for all hidden layer, saying n[1], n[2], ... n[l-1]
for unit_number in hidden_layer_units: # hidden_layer_units = [n[1], n[2], ..., n[l-1]]
n_current = unit_number
b.append(np.zeros((n_current, 1)))
W.append(np.random.randn(n_current, n_last)*0.01)
n_last = n_current
# for last ouput layer n[l]
b.append(np.zeros((Y.shape[0], 1)))
W.append(np.random.randn(Y.shape[0], n_last)*0.01)
return b, W
# build model by put all together
def model(X, Y, hidden_layer_units=[4], learning_rate=0.005, iterate_times=1000, print_cost=True):
layer_number = len(hidden_layer_units)+1
b, W = inital_params(X, Y, hidden_layer_units)
costs = []
for i in range(iterate_times):
A = forward(X, b, W, layer_number)
db, dW = backward(W, A, Y, layer_number)
b, W = update_params(db, dW, b, W, learning_rate, layer_number)
if print_cost and i%1000 == 0:
cost = cal_cost(A[layer_number], Y)
costs.append(cost)
print("cost after " + str(i) + " iterations: " + str(cost))
model_paras = {'b':b,
'W':W,
'costs':costs}
return model_paras
# predict Y based on model, Y is either 0 or 1
def predict(X, b, W):
layer_number = len(b)-1
A = forward(X, b, W, layer_number)
Y = np.round(A[-1])
return Y
# evaluate model with visulization
def evaluate(X, Y, b, W):
predictions = predict(X, b, W)
accuracy = float((np.dot(Y, predictions.T) + np.dot(1 - Y, 1 - predictions.T)) / float(Y.size) * 100)
return accuracy
Case Application
The model we build is suitable for all binary classification problem. And it’s structure is configurable in hidden_layer parameter. Asuming we could get training data from load_dataset() function, then the regular way to apply our model is:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16# set parameter for learning, those are the super parameters you can tune.
hidden_layer_units = [4]
learning_rate = 1.2
iterate_times = 10000
# load training data
X, Y = load_dataset()
# build model
model_paras = model(X, Y, hidden_layer_units, learning_rate, iterate_times)
b = model_paras['b']
W = model_paras['W']
# evaludate model
accuracy = evaluate(X, Y, b, W)
print ('Accuracy: %d ' % accuracy + '%')
Other framework
You could implement the equivalent model with framework easily. two of the frameworks are tensorflow and keras.
tensorflow
the key functions to implement the same model in tensorflow are like following. As you can see from the code, all you need to care is the forward part, tensorflow would take care of the backward part automaticlly since it stored the flow graph of all the units as sessions.1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75def initialize_parameters():
tf.set_random_seed(1) # so that your "random" numbers match ours
W1 = tf.get_variable("W1", [25, 12288], initializer=tf.contrib.layers.xavier_initializer(seed=1))
b1 = tf.get_variable("b1", [25, 1], initializer=tf.zeros_initializer())
W2 = tf.get_variable("W2", [12, 25], initializer=tf.contrib.layers.xavier_initializer(seed=1))
b2 = tf.get_variable("b2", [12, 1], initializer=tf.zeros_initializer())
W3 = tf.get_variable("W3", [6, 12], initializer=tf.contrib.layers.xavier_initializer(seed=1))
b3 = tf.get_variable("b3", [6, 1], initializer=tf.zeros_initializer())
parameters = {"W1": W1,"b1": b1,"W2": W2,"b2": b2,"W3": W3,"b3": b3}
return parameters
def forward_propagation(X, parameters):
# Retrieve the parameters from the dictionary "parameters"
W1 = parameters['W1']
b1 = parameters['b1']
W2 = parameters['W2']
b2 = parameters['b2']
W3 = parameters['W3']
b3 = parameters['b3']
### START CODE HERE ### (approx. 5 lines) # Numpy Equivalents:
Z1 = tf.add(tf.matmul(W1, X), b1) # Z1 = np.dot(W1, X) + b1
A1 = tf.nn.relu(Z1) # A1 = relu(Z1)
Z2 = tf.add(tf.matmul(W2, A1), b2) # Z2 = np.dot(W2, a1) + b2
A2 = tf.nn.relu(Z2) # A2 = relu(Z2)
Z3 = tf.add(tf.matmul(W3, A2), b3)
return Z3
def compute_cost(Z3, Y):
# to fit the tensorflow requirement for tf.nn.softmax_cross_entropy_with_logits(...,...)
logits = tf.transpose(Z3)
labels = tf.transpose(Y)
cost = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(logits=logits, labels=labels))
return cost
def model(X_train, Y_train, X_test, Y_test, learning_rate = 0.0001,
num_epochs = 1500, minibatch_size = 32, print_cost = True):
# Create Placeholders of shape (n_x, n_y)
X, Y = create_placeholders(n_x, n_y)
# Initialize parameters
parameters = initialize_parameters()
# Forward propagation: Build the forward propagation in the tensorflow graph
Z3 = forward_propagation(X, parameters)
# Cost function: Add cost function to tensorflow graph
cost = compute_cost(Z3, Y)
# Backpropagation: Define the tensorflow optimizer. Use an AdamOptimizer.
optimizer = tf.train.AdamOptimizer(learning_rate=learning_rate).minimize(cost)
# Initialize all the variables
init = tf.global_variables_initializer()
# Start the session to compute the tensorflow graph
with tf.Session() as sess:
# Run the initialization
sess.run(init)
_ , cost = sess.run([optimizer, cost], feed_dict={X:X, Y:Y})
# lets save the parameters in a variable
parameters = sess.run(parameters)
print ("Parameters have been trained!")
return parameters
keras
Keras is a higher level framework than tensorflow, it provided many more useful functions for implementing CNN and RNN. Basicly, you could apply it to build a model with only few line of code as it take care of both forward and backward part for common models, it’s basic block is layer, you could choose the provided layer to stack your model quickly.
The key code for building the same model we did before is:1
2
3
4
5
6
7
8
9from keras.layers import Input, Dense, Activation
X_input = Input(input_shape)
X_hidden = Dense(4, activation='sigmoid', name='fullycon1')(X_input)
Y = Dense(1, activation='sigmoid', name='fullycon2')(X_hidden)
model = Model(inputs=X_input, outputs=Y, name='fullycon_model')
model.compile(optimizer='adam', loss='mean_squared_error', metrics=["accuracy"])
model.fit(x=X_train, y=Y_train, epochs=10, batch_size=100)
Questions:
History:
- 2019-02-06: create post and draft based on my notebook.